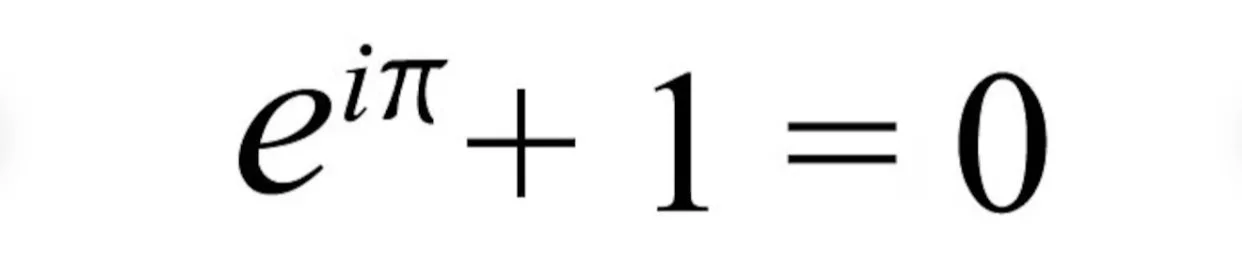05/07/2023
Becoming Euler’s Identity
depth vs. breadth
Euler's identity is a famous mathematical equation that relates five fundamental mathematical constants: the number 0, the number 1, the imaginary unit i, the mathematical constant π (pi), and the mathematical constant e. It is expressed as:
In this equation, e represents Euler's number*, which is an irrational and transcendental number approximately equal to 2.71828. The symbol i represents the imaginary unit**, defined as the square root of -1. And π (pi) represents the mathematical constant that represents the ratio of a circle's circumference to its diameter, approximately equal to 3.14159.
Euler's identity is remarkable because it not only combines these five fundamental mathematical constants (0, 1, e, i, π) in a single equation, connecting concepts from different branches of mathematics, including complex numbers, trigonometry, and exponential functions.
It has been described as one of the most beautiful equations in mathematics due to its elegant simplicity covering multiple concepts and deep connections to various mathematical fields.
An inch deep and a mile wide? Or a mile deep and an inch wide?
I ponder (and write) about the delicate equilibrium between breadth and depth quite a bit. This topic has been the subject of discourse in both industry and academic communities I am part of. People passionately argue in favour of either depth or breadth, each championing its unique significance and inherent value. Usually their respective arguments are coloured with confirmation bias – motivated reasoning behind their choices to rationalize their respective careers and actions.
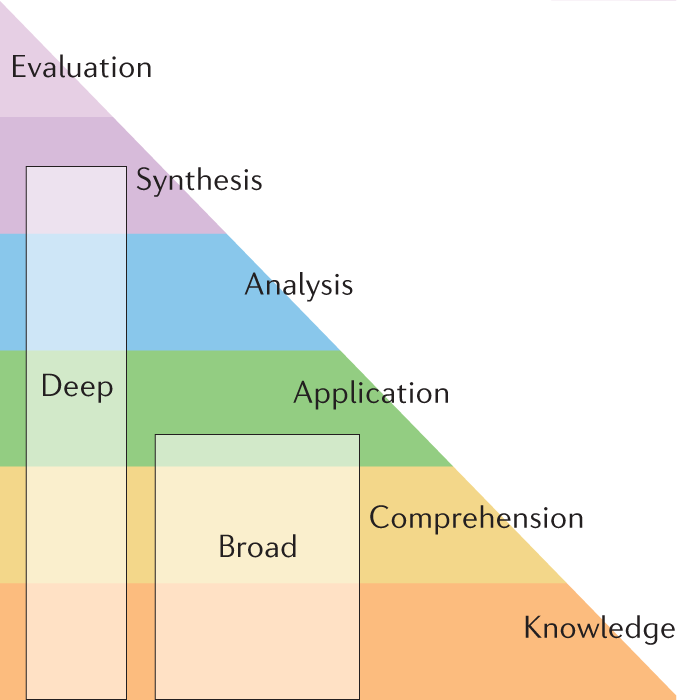
A hierarchical representation of Bloom’s Taxonomy is overlaid with hypothetical deep and broad courses with similar levels of content. Nature
The hierarchical figure illustrates the breadth and depth of topic coverage in a degree emphasizing different relationships to knowledge for students.
This also is consistently debated in the education world – Is it better to expose students to many concepts (breadth) or to foster a deeper exploration into fewer topics (depth)? Unsurprisingly, consensus has not been reached, but certainly the trend in the past decade is towards deeper learning.
In today's classrooms across various subjects, you will witness a greater emphasis on "messier" learning compared to previous years. Teachers and students now frequently collaborate to explore content areas in a more open-ended and exploratory manner. In this approach, equal importance is placed on the process and journey of learning alongside the final outcomes. As a result, collaboration among students (working in pairs or teams) and self-reflection have become more prevalent, as students inquire into why and how they approach their learning activities.
However, achieving mastery or even competency presents challenges. It is crucial to define what we mean by mastery and how we can determine when a student has reached it. This requires setting clear benchmarks and providing consistent, meaningful feedback. Teachers play a vital role in this process, investing significant effort in the initial planning stages and throughout the learning journey.
This tension between delving deeply into a subject versus covering a broader range of topics, along with the ongoing debate between teacher-directed instruction and student-directed learning, remains an important consideration.
Duality
I don’t want to find the “sweet spot”. I don’t want to find a “balance”. Why can’t we have duality? Why must we choose depth or breadth? Why does it have to be one or the other? Why must we either be a generalist or a specialist? A jack-of-all-trades or a master of none?
Why can’t we live in duality like Euler’s identity – in both the depth and the breadth, in the general and the special, in the all and the master?
I like the following proposal by JAMOE demonstrated through the lens of efficient note taking.
Start with breadth and then add depth.
Efficient learning involves strategically exploring promising sources and adopting a method akin to that of a jewel thief. It entails swiftly extracting valuable information, akin to smashing through a window and swiftly grabbing what is within reach. Through this approach, you acquire a handful of valuable insights.
By repeating this process, you gain the ability to identify locations rich in valuable ideas and evidence. Similar to a jewel thief, you can return to those sources to discreetly seize the most likely treasures hidden in the depths. You depart with a bag filled with valuable knowledge.
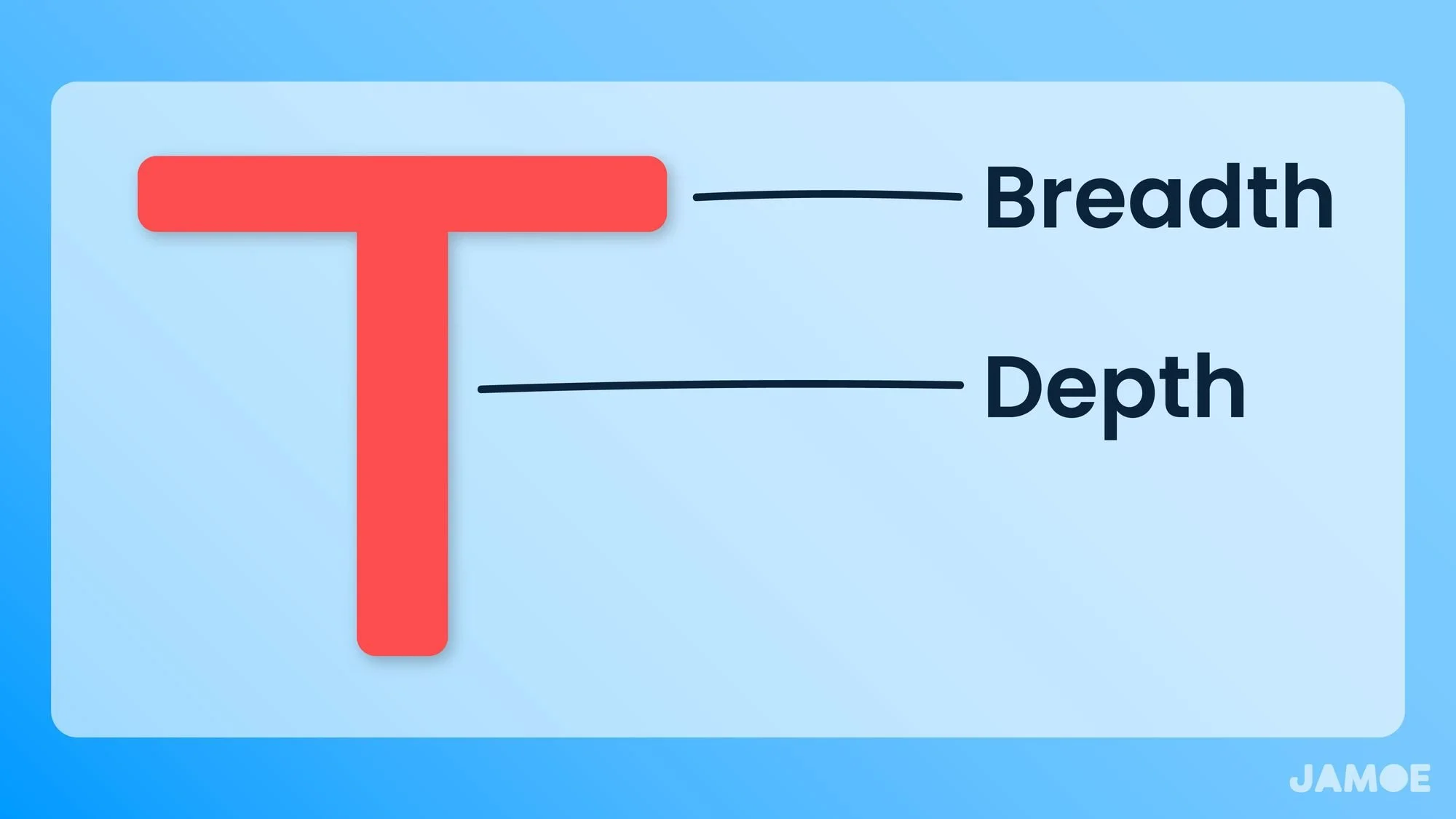
In essence, an effective learning strategy can be likened to a T-shape. It begins with breadth, represented by the arms of the T. This involves skimming the literature to grasp the larger context and overview. Subsequently, you transition to depth, represented by the stem of the T. Here, you delve into the most promising and relevant details, pushing your understanding and thinking to a deeper level.
Finding the richest rabbit holes. As you read, alternate between breadth and depth. By thinking fast and then slow, you'll be able to invest your time more efficiently.
What you want is your path to resemble a stack of Ts that converge at the point where you distinguish between truth and what appears to be true. Embracing this approach enhances efficacy, enabling you to swiftly sift through irrelevant details and locate the most fruitful rabbit holes to nourish your curiosity.
Just as Euler's identity beautifully unifies seemingly disparate mathematical concepts, we can strive for a harmonious integration of diverse skills and specialized knowledge.
Rather than viewing it as an either-or choice, we can aim for an approach that combines the advantages of both generalization and specialization. This mindset lets us cultivate a broad foundation of knowledge while also delving deeply into specific areas of interest or expertise.
By seeking a holistic understanding of various disciplines, we can develop a multidimensional perspective that fosters creativity, interdisciplinary problem-solving, and innovative thinking. We can leverage the power of specialization to gain in-depth expertise in specific fields, while simultaneously drawing upon the broader understanding of a generalist.
Living in this duality, embracing both depth and breadth, enables us to adapt to a rapidly changing world, contribute unique insights, and tackle complex challenges from multiple angles. It encourages a flexible and open mindset that embraces continuous learning and growth, fostering versatility and mastery across different domains.
Ultimately, by embracing both the general and the special, we can transcend the limitations of a dichotomous view and unlock new possibilities for personal and professional development.
This piece is 37/50 from my 50 days of writing series. Subscribe to hear about new posts.*Euler's number is an irrational and transcendental number, meaning it cannot be expressed as a finite fraction and its decimal representation goes on infinitely without repeating. The value of e has been calculated to millions of decimal places, and it is an essential constant in many areas of mathematics, science, and engineering.
The number e is significant because it arises naturally in various mathematical and scientific contexts. It appears in exponential growth and decay, compound interest calculations, probability theory, calculus, complex analysis, and many other mathematical applications. It is also intimately related to the natural logarithm function, which is the inverse function of exponentiation with base e.
**Complex numbers are numbers that extend the set of real numbers by introducing the imaginary unit, denoted as "i." An imaginary unit is defined as the square root of -1, which has no real number solution. Complex numbers are expressed in the form a + bi, where "a" and "b" are real numbers.
In a complex number, the real part (a) represents the traditional real numbers, while the imaginary part (bi) represents a multiple of the imaginary unit (i). The imaginary part allows for the representation of numbers that lie outside the real number line.